PhyPlan: Generalizable and Rapid Physical Task Planning with Physics-Informed Skill Networks for Robot Manipulators

......

Mudit Chopra^1*, Abhinav Barnawal^1*, Harshil Vagadia², Tamajit Banerjee², Shreshth Tuli², Souvik Chakraborty^1#, Rohan Paul^1#

¹Work primarily done when at IIT Delhi, ²Affiliated with IIT Delhi, ^*Indicate equal contribution, ^#Indicate equal advising,

Paper arXiv Video Code Data

PhyPlan is a novel physics-informed planning framework based on accelerated learning of Physical Reasoning Tasks using Physics Informed Skill Networks.

Abstract

Given the task of positioning a ball-like object to a goal region beyond direct reach, humans can often throw, slide, or rebound objects against the wall to attain the goal. However, enabling robots to reason similarly is non-trivial. Existing methods for physical reasoning are data-hungry and struggle with complexity and uncertainty inherent in the real world. This paper presents PhyPlan, a novel physics-informed planning framework that combines physics-informed neural networks (PINNs) with modified Monte Carlo Tree Search (MCTS) to enable embodied agents to perform dynamic physical tasks. PhyPlan leverages PINNs to simulate and predict outcomes of actions in a fast and accurate manner and uses MCTS for planning. It dynamically determines whether to consult a PINN-based simulator (coarse but fast) or engage directly with the actual environment (fine but slow) to determine optimal policy. Given an unseen task, PhyPlan can infer the sequence of actions and learn the latent parameters, resulting in a generalizable approach that can rapidly learn to perform novel physical tasks. Evaluation with robots in simulated 3D environments demonstrates the ability of our approach to solve 3D-physical reasoning tasks involving the composition of dynamic skills. Quantitatively, PhyPlan excels in several aspects: (i) it achieves lower regret when learning novel tasks compared to the state-of-the-art, (ii) it expedites skill learning and enhances the speed of physical reasoning, (iii) it demonstrates higher data efficiency compared to a physics un-informed approach.

Approach Overview

PhyPlan pipeline: Clockwise from top. (1) The robot learns a model of physical skills such as hitting, swinging, sliding etc. using a Physics-Informed Neural Network (PINN). The network incorporates a coarse physics governing equation in its loss function and can predict the future trajectory of the interacting object as well as the latent physical parameters of the domain. Given a new task (2), a Monte-Carlo Tree Search (MCTS) (3) searches for a plan by exploring the space of skill compositions, i.e., sampling over continuous parameters e.g., the height of object release, the angle of a wedge with which the object may collide. Simulating the trajectories during physical interaction using a forward pass of a PINN is faster than simulating rich inter-object dynamic interactions in a high-fidelity physics simulator (with complex physical models). The MCTS plan search (4) periodically balances sampling with the PINNs with occasional rollouts in the high-fidelity simulator. The discrepancy in the reward between (i) predicted by PINN rollouts and rollout in the physics simulator is modelled using a Gaussian Process (GP) that guides the MCTS towards the correct plan.

Skill Learning

We consider the problem of learning a model for physical skills such as bouncing a ball-like object off a wedge, sliding over an object, swinging a pendulum, throwing an object as a projectile and hitting an object with a pendulum. The skill learning model predicts the state trajectory of an object as it undergoes a dynamic interaction with another objects.

Sliding Skill

Skill network learns to determine the displacement and velocity of a sliding box with given initial velocity at any time queried on a rough plane

Throwing Skill

Skill network learns to determine the location and velocity of ball thrown with given initial angle and velocity at any time queried.

Swinging Skill

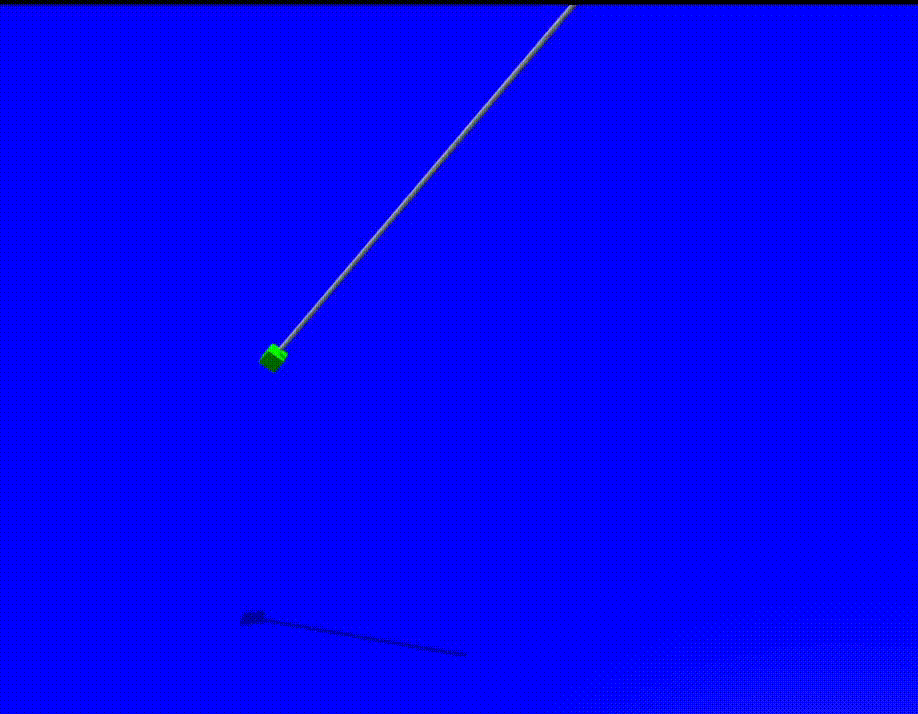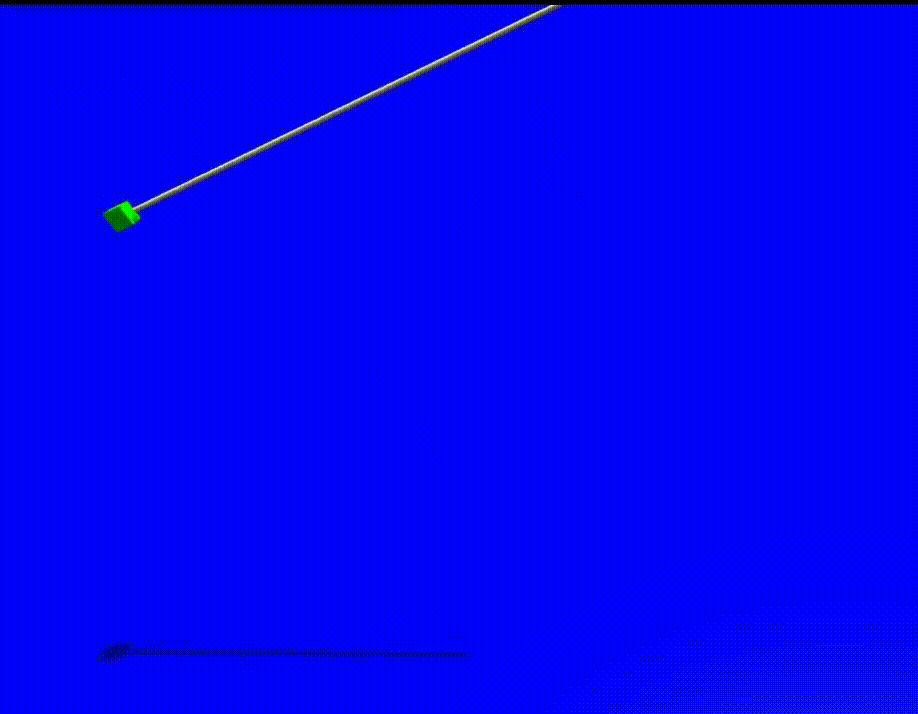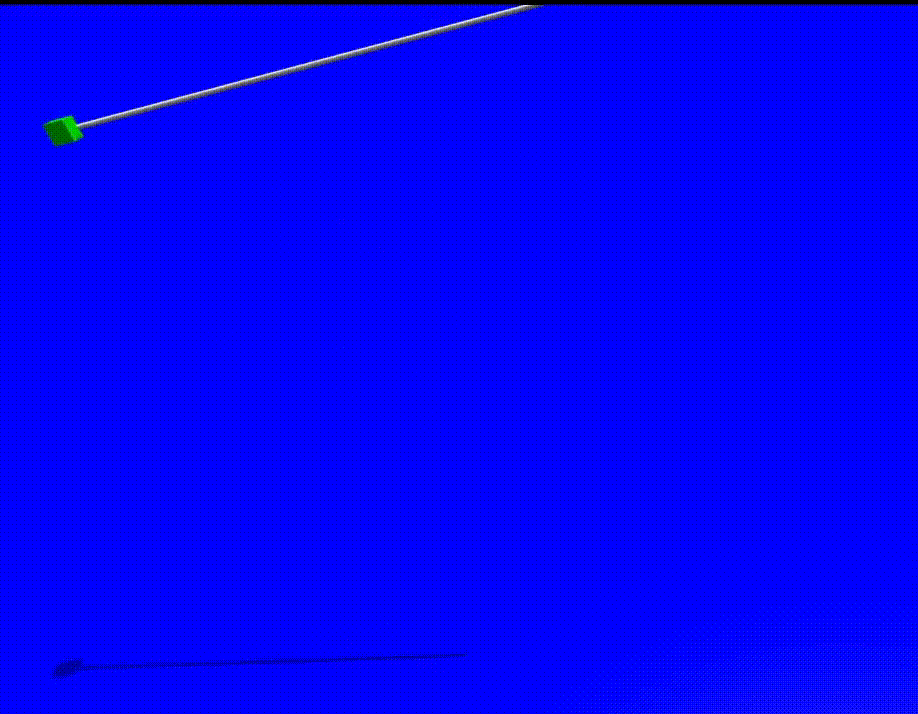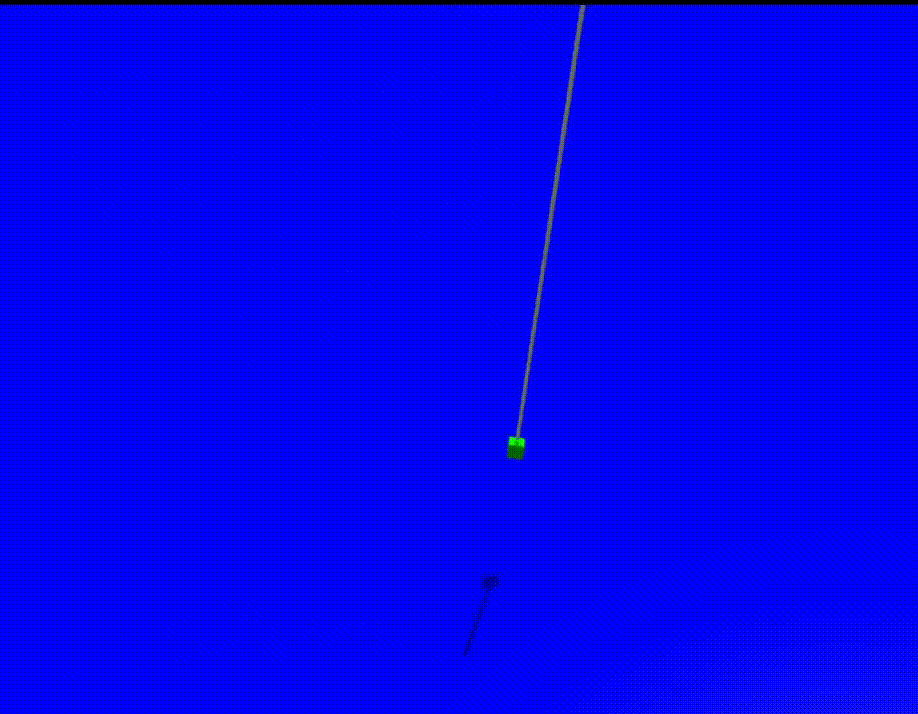
Skill network learns to determine angular position and angular velocity of pendulum at any time queried with given initial angular position.

Hitting Skill

Skill network learns to determine velocity of puck just after it gets hit by a swinging pendulum.

Bouncing Skill

Skill network learns to determine velocity of ball just after it bounces a wedge.

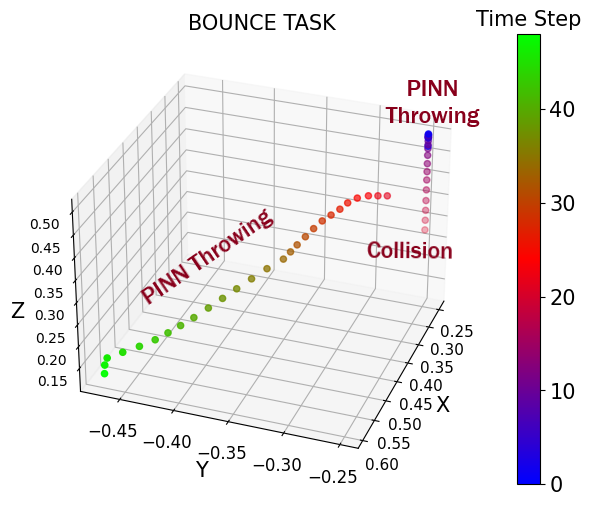
The skill learning model is based on a neural network that predicts the object's state during dynamic interaction continuously parameterised by time. The figure on the side shows the predicted positions of the ball plotted against time in the Bounce Task. Such interactions can be simulated in a physics engine by using numerical integration schemes. However, since we aim to perform multi-step interactions, simulating outcomes during training is often intractable. Hence, we adopt a learning-based approach and learn a function which predicts the object's state during dynamic interaction continuously parameterised by time. For certain skills like swining, sliding and throwing we levarage the known governing physics equations and employ a physics-informed loss function in neural network to constrain the latent space, these are called as Physics-Informed Skill Networks. However, skills like bouncing and hitting are learnt directly from data because of complex and intractable physics.

Physical Reasoning Tasks

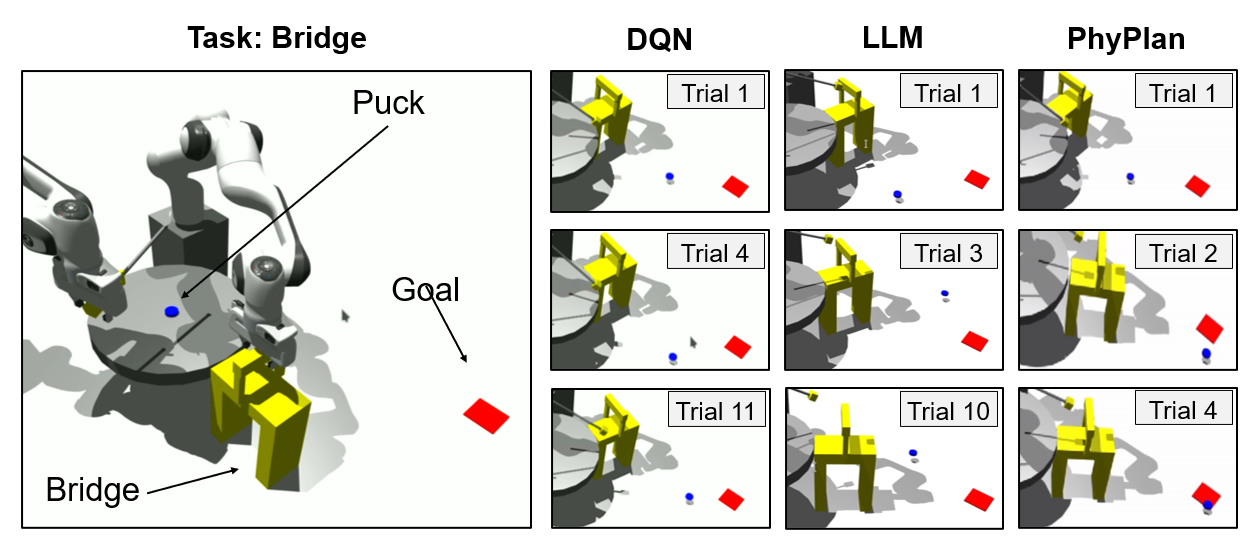
We created the following four challenging 3D physical reasoning tasks to analyse the performance of PhyPlan, inspired by prior works in simplistic 2D environments presnted in [Allen et al., 2020] and [Bakhtin et al., 2019]. PhyPlan performs semantic reasoning using PINN-based Skill Models before executing each action in the environemnt (just as Humans think before executing). It also learns the difference between PINN-based rewards for actions and actual rewards as it executes actions (called online learning). Therefore, it often improves in subsequent actions (Just as Humans improve their actions with more trials). The videos show the actions taken by PhyPlan on each task. The effect of online learning is more evident in Bounce and Bridge tasks where the robot fails to perform well in early attempts.

Launch Task

Robot trains to use the pendulum object present in the environment to make the ball reach the goal

The robot learns to correctly align the pendulum's plane and angle to throw the ball into the box.

Slide Task

Robot trains to use pendulum object present in the environment to slide the puck to the goal

The following five trials represent the robot eventually sliding the puck to reach the goal by aligning the pendulum and using physical skills like hitting and sliding.

Bounce Task

Robot trains to use wedge object present in the environment to make the ball reach the goal

In the above five trials, the robot places the wedge at the correct location with the proper orientation, throwing the ball from the proper height, accomplishing the ball reaching the goal.

Bridge Task

Robot trains to use the pendulum and bridge objects present in the environment to make the puck reach the goal

Over the shown trials, the robot learns to correctly align the pendulum so that the hitting plane is correctly aligned. Eventually, the robot effectively uses objects like the bridge present in the environment.

LLM (Baseline) Prompting Details

We investigate the physical reasoning abilities of a Large Language Model (specifically Google's Gemini-Pro LLM). We initially describe the task setup and ask the LLM to generate the actions. We execute the generated action in the environemnt and reprompt the LLM based with the feedback of where the ball/puck landed with respect to the goal.

Launch Task

Initial Prompt (Task Description):

There is a robot and a goal located at {goal_pos} outside the direct reach of the robot. There is a ball that needs to reach the goal. The environment has a fixed pillar over which the ball is resting, and a pendulum hanging over the ball that the robot can orient to hit the ball to throw it to the goal. The robot can orient the pendulum along any vertical plane and choose to drop the pendulum from any angle from the vertical axis. When hit with a pendulum, the puck projectiles and lands far away on the ground.
Sanity check 1: How does the plane of the pendulum affect the puck's position with respect to the goal?
Sanity check 2: How does the drop angle of the pendulum affect the puck's position with respect to the goal?

Feedback Prompt:

In one line, give the numerical values of the angle to orient the pendulum's plane and the angle to drop the pendulum from (both in decimal radians). The bound for plane orientation angle is ({bnds[0][0]}, {bnds[0][1]}) and that for drop angle with vertical axis is ({bnds[1][0]}, {bnds[1][1]}). I will tell you where the ball landed, and you should modify your answer accordingly till the ball reaches the goal. I have marked the ground into two halves. The goal lies in one half, and the robot and the wedge are at the centre. Thoughout the conversation, remember that my response would be one of these:
  1. The ball lands in the half not containing goal, I'd say 'WRONG HALF'.
  2. The ball lands in the correct half but left of the goal, I'd say 'LEFT by <horizontal distance between ball and goal>'.
  3. The ball lands in the correct half but right of the goal, I'd say 'RIGHT by <horizontal distance between ball and goal>'.
  4. The ball lands in the correct half and in line but overshot the goal, I'd say 'OVERSHOT by <horizontal distance between ball and goal>'.
  5. The ball lands in the correct half and in line but fell short of the goal, I'd say 'FELL SHORT by <horizontal distance between ball and goal>'.
  6. Finally, the ball successfully landed in the goal, I'd say 'GOAL'. \
Note: In your response, do not write anything else except the (pendulum's plane angle, pendulum's drop angle) pair. Send in tuple FORMAT: (angle 1, angle 2). Do not emphasise the answer, just return plain text. Let's begin with an initial guess!

Slide Task

Initial Prompt (Task Description):

There is a robot and a goal located at {goal_pos} outside the direct reach of the robot. There is a puck that needs to reach the goal. The environment has a fixed table over which the puck slides, and a pendulum hanging over the puck that the robot can orient to hit the puck to slide it to the goal. The robot can orient the pendulum along any vertical plane and choose to drop the pendulum from any angle from the vertical axis. When hit with a pendulum, the puck slides on the table.
Sanity check 1: How does the plane of the pendulum affect the puck's position with respect to the goal?
Sanity check 2: How does the drop angle of the pendulum affect the puck's position with respect to the goal?

Feedback Prompt:

In one line, give the numerical values of the angle to orient the pendulum's plane and the angle to drop the pendulum from (both in decimal radians). The bound for plane orientation angle is ({bnds[0][0]}, {bnds[0][1]}) and that for drop angle with vertical axis is ({bnds[1][0]}, {bnds[1][1]}). I will tell you where the puck landed, and you should modify your answer accordingly till the puck reaches the goal. I have marked the ground into two halves. The goal lies in one half, and the robot and the wedge are at the centre. Thoughout the conversation, remember that my response would be one of these:
  1. The puck lands in the half not containing goal, I'd say 'WRONG HALF'.
  2. The puck lands in the correct half but left of the goal, I'd say 'LEFT by <horizontal distance between puck and goal>'.
  3. The puck lands in the correct half but right of the goal, I'd say 'RIGHT by <horizontal distance between puck and goal>'.
  4. The puck lands in the correct half and in line but overshot the goal, I'd say 'OVERSHOT by <horizontal distance between puck and goal>'.
  5. The puck lands in the correct half and in line but fell short of the goal, I'd say 'FELL SHORT by <horizontal distance between puck and goal>'.
  6. Finally, the puck successfully landed in the goal, I'd say 'GOAL'. \
Note: In your response, do not write anything else except the (pendulum's plane angle, pendulum's drop angle) pair. Send in tuple FORMAT: (angle 1, angle 2). Do not emphasise the answer, just return plain text. Let's begin with an initial guess!

Bounce Task

Initial Prompt (Task Description):

There is a robot and a goal located at {goal_pos} outside the direct reach of the robot. There is a ball that needs to reach the goal. The environment has a wedge (an inclined plane at 45 degrees from the horizontal plane) placed at origin, and the robot can bounce the ball over the wedge to place the ball inside the goal. The height of the wedge centre from the ground is fixed at 0.3 metres. The robot can orient the wedge along any horizontal direction and choose to drop the ball over the wedge from any height. When dropped from a height, the ball bounces on the wedge and lands far away on the ground.
Sanity check 1: How does the orientation angle of the wedge affect the ball's position with respect to the goal?
Sanity check 2: How does the drop height of the ball affect the ball's position with respect to the goal?

Feedback Prompt:

In one line, give the numerical values of the angle to orient the wedge and the height to drop the ball from in the format (angle in decimal radians, height in meters). The bound for angle is ({bnds[0][0]}, {bnds[0][1]}) and that for height is ({bnds[1][0]}, {bnds[1][1]}). I will tell you where the ball landed, and you should modify your answer accordingly till the ball reaches the goal. I have marked the ground into two halves. The goal lies in one half, and the robot and the wedge are at the centre. Thoughout the conversation, remember that my response would be one of these:
    1. The ball lands in the half not containing goal, I'd say 'WRONG HALF'.
    2. The ball lands in the correct half but left of the goal, I'd say 'LEFT by <horizontal distance between ball and goal>'.
    3. The ball lands in the correct half but right of the goal, I'd say 'RIGHT by <horizontal distance between ball and goal>'.
    4. The ball lands in the correct half and in line but overshot the goal, I'd say 'OVERSHOT by <horizontal distance between ball and goal>'.
    5. The ball lands in the correct half and in line but fell short of the goal, I'd say 'FELL SHORT by <horizontal distance between ball and goal>'.
    6. Finally, the ball successfully landed in the goal, I'd say 'GOAL'.
Note: In your response, do not write anything else except the (angle, height) pair. Send in tuple FORMAT: (angle, height). Do not emphasise the answer, just return plain text. Let's begin with an initial guess!

Bridge Task

Initial Prompt (Task Description):

There is a robot and a goal located at {goal_pos} outside the direct reach of the robot. There is a puck that needs to reach the goal. The environment has a fixed table over which the puck slides, a movable bridge over which the puck slides and a pendulum that the robot can orient to move the puck towards the goal. The robot can orient the pendulum along any vertical plane, orient the bridge in any horizontal direction and choose to drop the pendulum from any angle from the vertical axis. When hit with a pendulum, the puck slides on the table, then on the bridge and finally projectiles to land far away on the ground.
Sanity check 1: How does the plane of the pendulum affect the puck's position with respect to the goal?
Sanity check 2: How does the drop angle of the pendulum affect the puck's position with respect to the goal?
Sanity check 3: How does the orientation angle of the bridge affect the puck's position with respect to the goal?

Feedback Prompt:

In one line, give the numerical values of the angle to orient the pendulum's plane, the angle to orient the bridge and the angle to drop the pendulum from (all in decimal radians). The bound for plane orientation angle is ({bnds[0][0]}, {bnds[0][1]}), that for bridge orientation angle is ({bnds[2][0]}, {bnds[2][1]}), and that for drop angle with vertical axis is ({bnds[1][0]}, {bnds[1][1]}). I will tell you where the puck landed, and you should modify your answer accordingly till the puck reaches the goal. I have marked the ground into two halves. The goal lies in one half, and the robot and the wedge are at the centre. Thoughout the conversation, remember that my response would be one of these:
  1. The puck lands in the half not containing goal, I'd say 'WRONG HALF'.
  2. The puck lands in the correct half but left of the goal, I'd say 'LEFT by <horizontal distance between puck and goal>'.
  3. The puck lands in the correct half but right of the goal, I'd say 'RIGHT by <horizontal distance between puck and goal>'.
  4. The puck lands in the correct half and in line but overshot the goal, I'd say 'OVERSHOT by <horizontal distance between puck and goal>'.
  5. The puck lands in the correct half and in line but fell short of the goal, I'd say 'FELL SHORT by <horizontal distance between puck and goal>'.
  6. Finally, the puck successfully landed in the goal, I'd say 'GOAL'.
Note: In your response, do not write anything else except the (pendulum's plane angle, pendulum's drop angle, bridge's orientation angle) triplet. Send in tuple FORMAT: (angle 1, angle 2, angle 3). Do not emphasise the answer, just return plain text. Let's begin with an initial guess!

Comparison with the Baselines

Below is a qualitative comparison with the baselines "DQN" (adapted from [Bakhtin et al., 2019]) and LLM. DQN is a Deep Q-Network trained on a set of observation-action-reward triplets minimizing the cross-entropy between the soft prediction and the observed reward. DQN also uses the same algorithm (Gaussian Process) as PhyPlan for online learning (here)

DQN (Baseline) executes actions in sequence while learning the difference in the predicted reward for an action and the actual reward. However, it does not use the bridge even after 11 trials which is needed to land the ball further closer to the goal.
LLM (Baseline) executes actions in sequence while correcting them based on feedback in further trials. It uses the bridge in a few trials but does align the pandulum appropriately even in 10 trials.
PhyPlan executes actions in sequence while learning the difference in the predicted reward for an action and the actual reward. It does not use the bridge in the first attempt because of errors in prediction. However, it quickly realises the need of the bridge in the second attempt. Further, it chooses appropriate actions to land the ball in the goal in just the fourth attempt. Note that the robot learns to use the bridge effectively; a physical reasoning task reported earlier [Allen et al., 2020] to be challenging to learn for model-free methods, highlighting PhyPlan’s adaptability to long-horizon tasks.

References

1. [Allen et al., 2020] Kelsey R Allen, Kevin A Smith, and Joshua B Tenenbaum.
        Rapid trial-and-error learning with simulation supports flexible tool use and physical reasoning.
        Proceedings of the National Academy of Sciences, 117(47):29302–29310, 2020.

2. [Bakhtin et al., 2019] Anton Bakhtin, Laurens van der Maaten, Justin Johnson, Laura Gustafson, and Ross Girshick.
        Phyre: A new benchmark for physical reasoning.
        Advances in Neural Information Processing Systems, 32,484 2019.

Citation

@inproceedings{phyplan2024,
      title     = {PhyPlan: Compositional and Adaptive Physical Task Reasoning with Physics-Informed Skill Networks for Robot Manipulators},
      author    = {Chopra, Mudit and Barnawal, Abhinav and Vagadia, Harshil and Banerjee, Tamajit and Tuli, Shreshth and Chakraborty, Souvik and Paul, Rohan},
      booktitle = {},
      year      = {2024}
    }